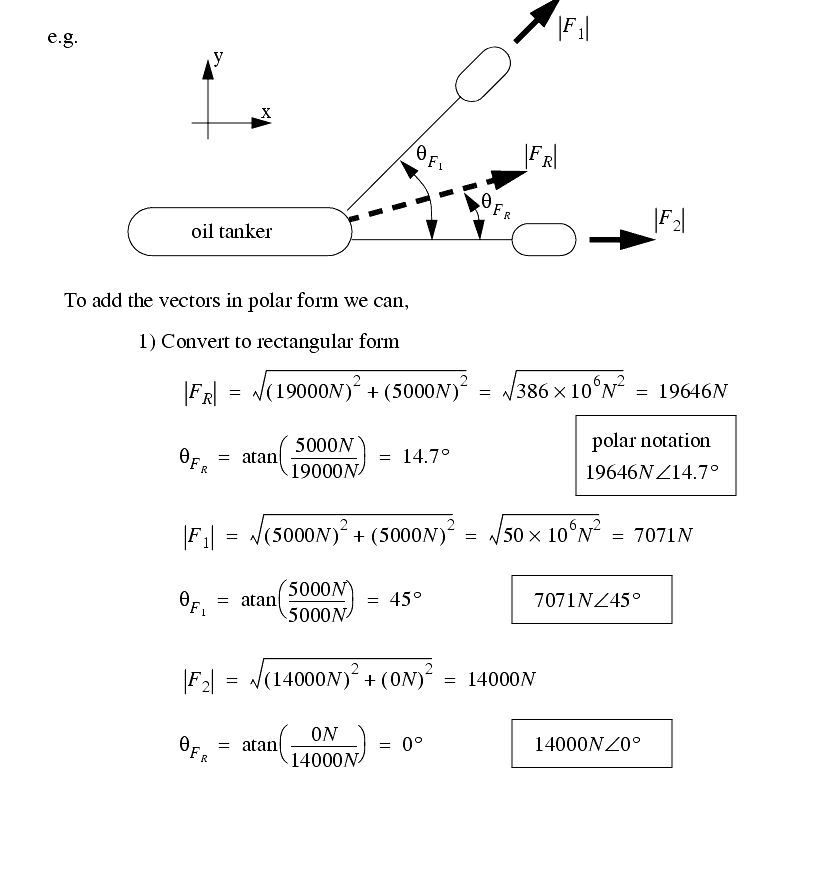
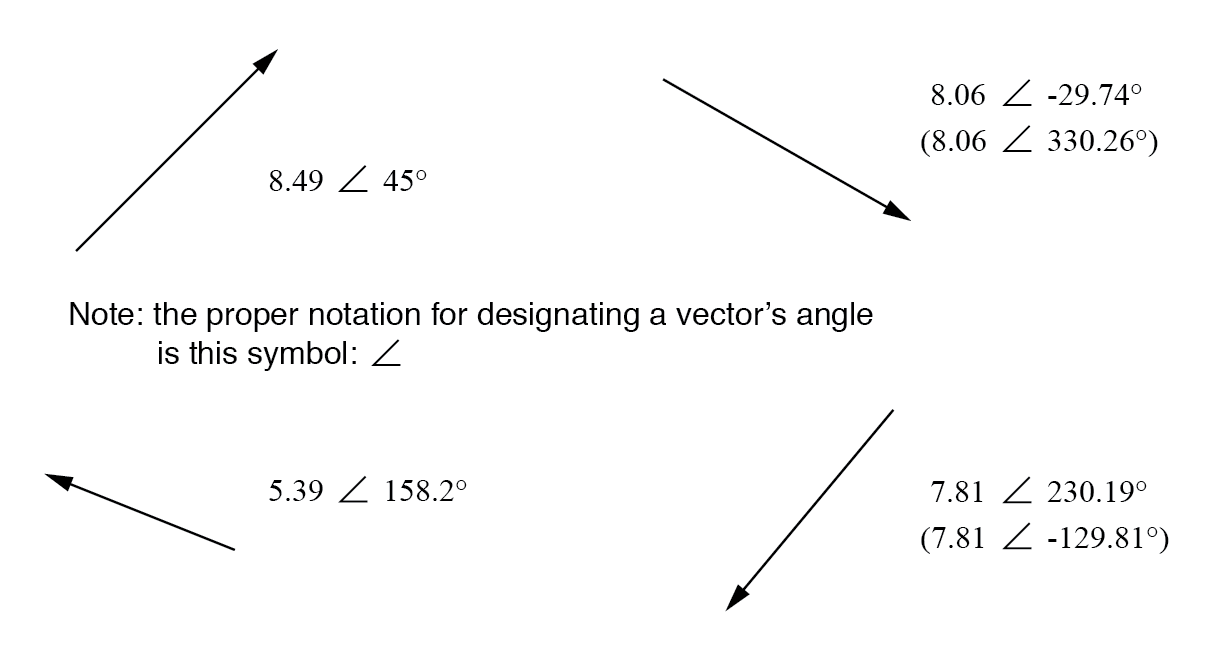
Polar Form Vectors
Polar Form Vectors - Next, we draw a line straight down from the arrowhead to the x axis. The sum of (2,4) and (1,5) is (2+1,4+5), which is (3,9). Similarly, the reactance of the inductor, j50, can be written in polar form as , and the reactance of c 2, −j40, can be written in polar form as. A complex number in the polar form will contain a magnitude and an angle to. Substitute the vector 1, −1 to the equations to find the magnitude and the direction. Web the vector a is broken up into the two vectors ax and ay (we see later how to do this.) adding vectors we can then add vectors by adding the x parts and adding the y parts: X = r \cos \theta y = r \sin \theta let’s suppose we have two polar vectors: From the definition of the inner product we have. To convert a point or a vector to its polar form, use the following equations to determine the magnitude and the direction. Web answer (1 of 2):
Polar form of a complex number. Web calculus 2 unit 5: Let →r be the vector with magnitude r and angle ϕ that denotes the sum of →r1 and →r2. Examples of polar vectors include , the velocity vector ,. In summary, the polar forms are: Up to this point, we have used a magnitude and a direction such as 30 v @ 67°. Web polar form is where a complex number is denoted by the length (otherwise known as the magnitude, absolute value, or modulus) and the angle of its vector (usually denoted by an angle symbol that looks like this: M = x2 + y2− −−−−−√. Substitute the vector 1, −1 to the equations to find the magnitude and the direction. Web polar form when dealing with vectors, there are two ways of expressing them.
A polar vector (r, \theta) can be written in rectangular form as: In polar form, a vector a is represented as a = (r, θ) where r is the magnitude and θ is the angle. There's also a nice graphical way to add vectors, and the two ways will always result in the same vector. Web spherical vectors are specified like polar vectors, where the zenith angle is concatenated as a third component to form ordered triplets and matrices. Web answer (1 of 2): X = r \cos \theta y = r \sin \theta let’s suppose we have two polar vectors: The polar form can also be verified using the conversion equation. Web polar form is where a complex number is denoted by the length (otherwise known as the magnitude, absolute value, or modulus) and the angle of its vector (usually denoted by an angle symbol that looks like this: Let \(z = a + bi\) be a complex number. Web rectangular form breaks a vector down into x and y coordinates.
Polar Form of Vectors YouTube
Polar form of a complex number. Web rectangular form breaks a vector down into x and y coordinates. Web the vector a is broken up into the two vectors ax and ay (we see later how to do this.) adding vectors we can then add vectors by adding the x parts and adding the y parts: Web vectors in polar.
Converting Vectors between Polar and Component Form YouTube
A polar vector (r, \theta) can be written in rectangular form as: \[z = 2\left( {\cos \left( {\frac{{2\pi }}{3}} \right) + i\sin \left( {\frac{{2\pi }}{3}} \right)} \right)\] now, for the sake of completeness we should acknowledge that there are many more equally valid polar forms for this complex number. The vector (8, 13) and the vector (26, 7) add up.
polar form of vectors YouTube
Web to add the vectors (x₁,y₁) and (x₂,y₂), we add the corresponding components from each vector: Web let →r1 and →r2 denote vectors with magnitudes r1 and r2, respectively, and with angles ϕ1 and ϕ2, respectively. Note that for a vector ai + bj, it may be represented in polar form with r = (magnitude of vector), and theta =.
Vectors in polar form YouTube
Web to add the vectors (x₁,y₁) and (x₂,y₂), we add the corresponding components from each vector: Z is the complex number in polar form, a is the magnitude or modulo of the vector and θ is its angle or argument of a which can be either positive or negative. Web polar vectors are the type of vector usually simply known.
PPT Vectors and Polar Coordinates PowerPoint Presentation, free
Web the polar form is where a complex number is denoted by the length (otherwise known as the magnitude, absolute value, or modulus) and the angle of its vector (usually denoted by an angle symbol that looks like this: Web polar form is where a complex number is denoted by the length (otherwise known as the magnitude, absolute value, or.
eNotes Mechanical Engineering
The azimuth and zenith angles may be both prefixed with the angle symbol ( ∠ \angle ); Web the vector a is broken up into the two vectors ax and ay (we see later how to do this.) adding vectors we can then add vectors by adding the x parts and adding the y parts: Here, a x, a y,.
PPT Physics 430 Lecture 2 Newton’s 2 nd Law in Cartesian and Polar
Web rectangular form breaks a vector down into x and y coordinates. There's also a nice graphical way to add vectors, and the two ways will always result in the same vector. M = x2 + y2− −−−−−√. Web answer (1 of 2): Web polar vectors are the type of vector usually simply known as vectors. in contrast, pseudovectors (also.
Adding Vectors in Polar Form YouTube
Web key points a polar form of a vector is denoted by ( 𝑟, 𝜃), where 𝑟 represents the distance from the origin and 𝜃 represents the. \[z = 2\left( {\cos \left( {\frac{{2\pi }}{3}} \right) + i\sin \left( {\frac{{2\pi }}{3}} \right)} \right)\] now, for the sake of completeness we should acknowledge that there are many more equally valid polar forms.
2.5 Polar Form and Rectangular Form Notation for Complex Numbers
Thus, →r = →r1 + →r2. The azimuth and zenith angles may be both prefixed with the angle symbol ( ∠ \angle ); Let →r be the vector with magnitude r and angle ϕ that denotes the sum of →r1 and →r2. Web calculus 2 unit 5: Web polar form and cartesian form of vector representation polar form of vector.
Examples of multiplying and dividing complex vectors in polar form
Web spherical vectors are specified like polar vectors, where the zenith angle is concatenated as a third component to form ordered triplets and matrices. Web polar forms are one of the many ways we can visualize a complex number. Examples of polar vectors include , the velocity vector ,. A complex number in the polar form will contain a magnitude.
Web Key Points A Polar Form Of A Vector Is Denoted By ( 𝑟, 𝜃), Where 𝑟 Represents The Distance From The Origin And 𝜃 Represents The.
Thus, →r = →r1 + →r2. There's also a nice graphical way to add vectors, and the two ways will always result in the same vector. For more practice and to create math. The azimuth and zenith angles may be both prefixed with the angle symbol ( ∠ \angle );
Polar Form Of A Complex Number.
Web answer (1 of 2): The sum of (2,4) and (1,5) is (2+1,4+5), which is (3,9). In summary, the polar forms are: But there can be other functions!
\[Z = 2\Left( {\Cos \Left( {\Frac{{2\Pi }}{3}} \Right) + I\Sin \Left( {\Frac{{2\Pi }}{3}} \Right)} \Right)\] Now, For The Sake Of Completeness We Should Acknowledge That There Are Many More Equally Valid Polar Forms For This Complex Number.
Let \(z = a + bi\) be a complex number. Web calculus 2 unit 5: In this learning activity you'll place given vectors in correct positions on the cartesian coordinate system. A complex number in the polar form will contain a magnitude and an angle to.
The Components Of The Rectangular Form Of A Vector ⃑ 𝑣 = 𝑥 ⃑ 𝑖 + 𝑦 ⃑ 𝑗 Can Be Obtained From The Components Of The Polar.
Web let →r1 and →r2 denote vectors with magnitudes r1 and r2, respectively, and with angles ϕ1 and ϕ2, respectively. Let →r be the vector with magnitude r and angle ϕ that denotes the sum of →r1 and →r2. The first step to finding this expression is using the 50 v as the hypotenuse and the direction as the angle. Here, a x, a y, and a z are the coefficients (magnitudes of the vector a along axes after.