Transformer Formula Sheet

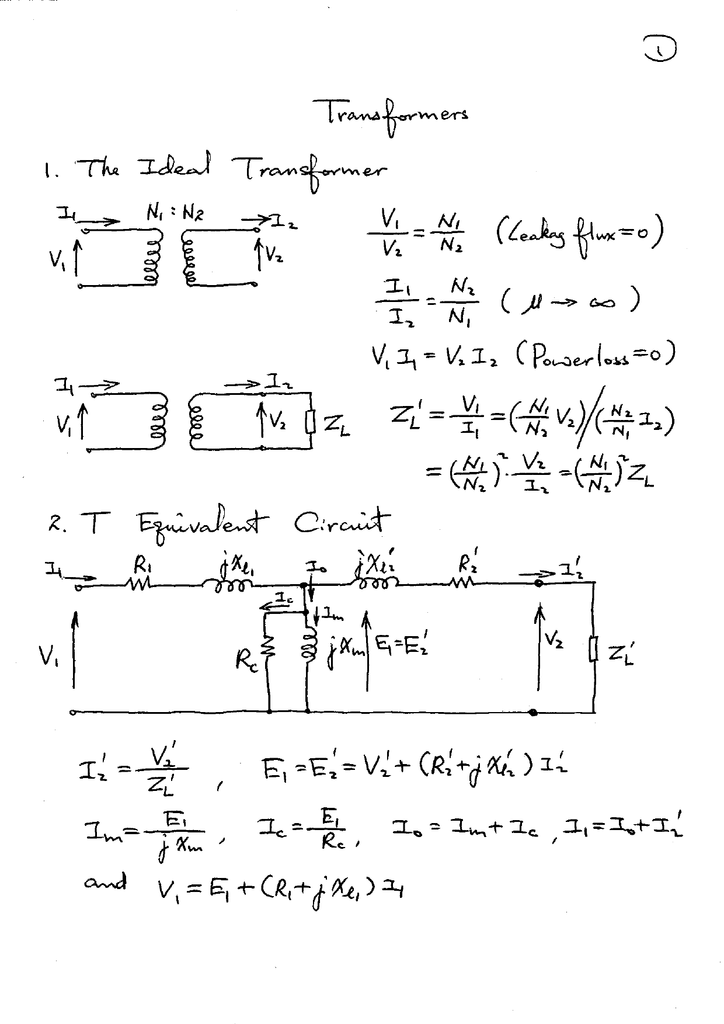
Transformer Formula Sheet - Web figure 1 as seen in figure 1, the transformer has two inductors: Equivalent resistance of transformer windings: A source (or primary) inductor (ls) and a load (or secondary) inductor (ll). \[v_{s} = \frac{n_{s}}{n_{p}} \times v_{p}\] where, \[n_{p}\] = number of turns in the primary \[n_{s}\] = number of. Web as the transformer is basically a linear device, a ratio now exists between the number of turns of the primary coil divided by the number of turns of the secondary coil. Each inductor loop is in. Emf induced in primary & secondary windings:

Web figure 1 as seen in figure 1, the transformer has two inductors: Web as the transformer is basically a linear device, a ratio now exists between the number of turns of the primary coil divided by the number of turns of the secondary coil. A source (or primary) inductor (ls) and a load (or secondary) inductor (ll). Equivalent resistance of transformer windings: Each inductor loop is in. Emf induced in primary & secondary windings: \[v_{s} = \frac{n_{s}}{n_{p}} \times v_{p}\] where, \[n_{p}\] = number of turns in the primary \[n_{s}\] = number of.

Web figure 1 as seen in figure 1, the transformer has two inductors: Equivalent resistance of transformer windings: A source (or primary) inductor (ls) and a load (or secondary) inductor (ll). Web as the transformer is basically a linear device, a ratio now exists between the number of turns of the primary coil divided by the number of turns of the secondary coil. Each inductor loop is in. Emf induced in primary & secondary windings: \[v_{s} = \frac{n_{s}}{n_{p}} \times v_{p}\] where, \[n_{p}\] = number of turns in the primary \[n_{s}\] = number of.

Simplifying the transformer equation YouTube

Equivalent resistance of transformer windings: Web as the transformer is basically a linear device, a ratio now exists between the number of turns of the primary coil divided by the number of turns of the secondary coil. \[v_{s} = \frac{n_{s}}{n_{p}} \times v_{p}\] where, \[n_{p}\] = number of turns in the primary \[n_{s}\] = number of. Emf induced in primary &.

Transformer Formula Sheet

Web figure 1 as seen in figure 1, the transformer has two inductors: \[v_{s} = \frac{n_{s}}{n_{p}} \times v_{p}\] where, \[n_{p}\] = number of turns in the primary \[n_{s}\] = number of. Emf induced in primary & secondary windings: A source (or primary) inductor (ls) and a load (or secondary) inductor (ll). Equivalent resistance of transformer windings:

Pin on Electrical

Equivalent resistance of transformer windings: Emf induced in primary & secondary windings: \[v_{s} = \frac{n_{s}}{n_{p}} \times v_{p}\] where, \[n_{p}\] = number of turns in the primary \[n_{s}\] = number of. Web figure 1 as seen in figure 1, the transformer has two inductors: Each inductor loop is in.

Current transformer (CT) saturation calculator EEP

Emf induced in primary & secondary windings: A source (or primary) inductor (ls) and a load (or secondary) inductor (ll). Web as the transformer is basically a linear device, a ratio now exists between the number of turns of the primary coil divided by the number of turns of the secondary coil. \[v_{s} = \frac{n_{s}}{n_{p}} \times v_{p}\] where, \[n_{p}\] =.

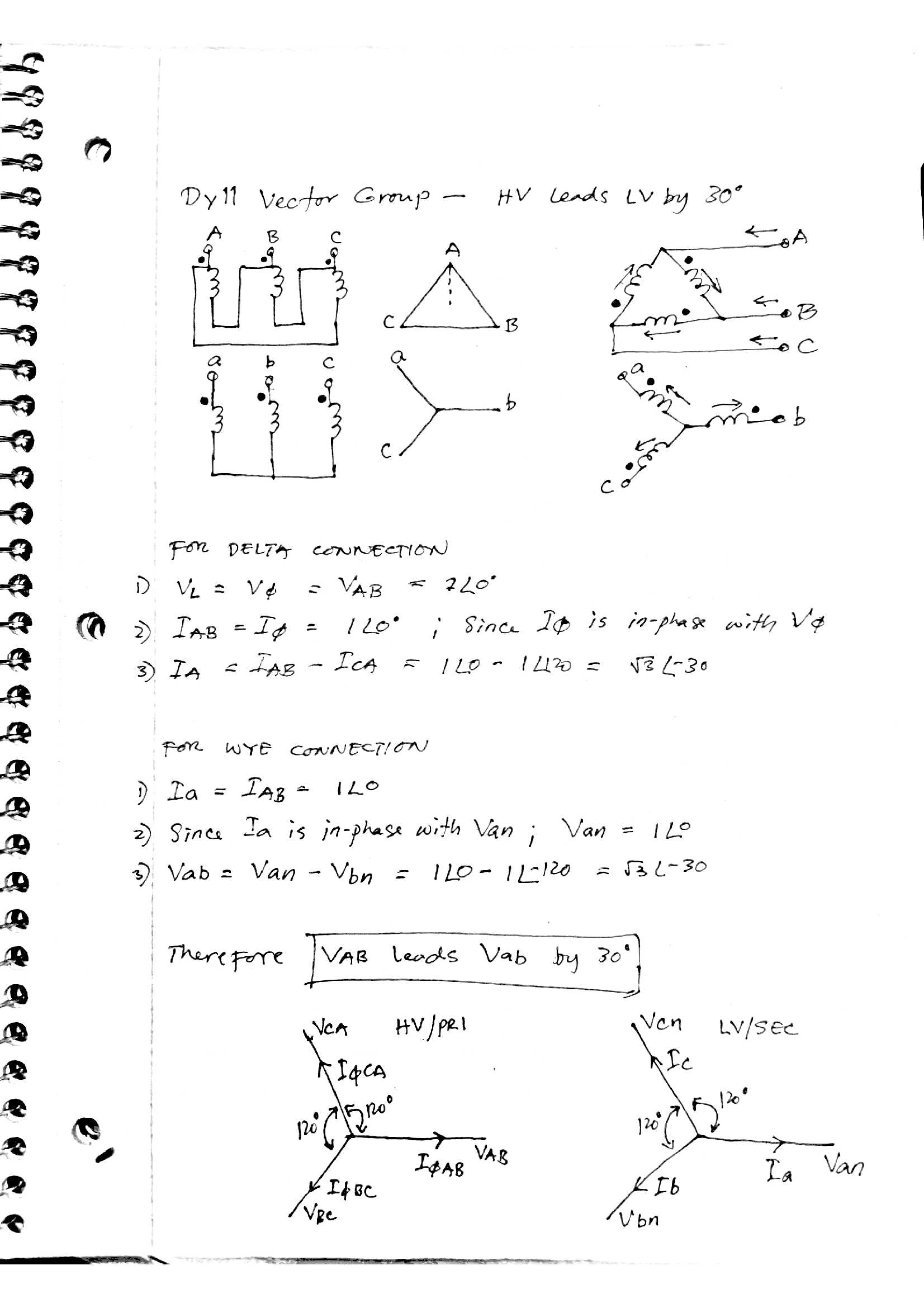
Transformer Vector Groups Basic Concepts Part 1 Electrical

Each inductor loop is in. Web figure 1 as seen in figure 1, the transformer has two inductors: Web as the transformer is basically a linear device, a ratio now exists between the number of turns of the primary coil divided by the number of turns of the secondary coil. \[v_{s} = \frac{n_{s}}{n_{p}} \times v_{p}\] where, \[n_{p}\] = number of.

Transformer Circuit and Equation YouTube

Emf induced in primary & secondary windings: Web figure 1 as seen in figure 1, the transformer has two inductors: Web as the transformer is basically a linear device, a ratio now exists between the number of turns of the primary coil divided by the number of turns of the secondary coil. A source (or primary) inductor (ls) and a.

Power And Distribution Transformers Sizing Calculations Part Eight

Web as the transformer is basically a linear device, a ratio now exists between the number of turns of the primary coil divided by the number of turns of the secondary coil. Equivalent resistance of transformer windings: Web figure 1 as seen in figure 1, the transformer has two inductors: \[v_{s} = \frac{n_{s}}{n_{p}} \times v_{p}\] where, \[n_{p}\] = number of.

Transformer Calculation Sheet

\[v_{s} = \frac{n_{s}}{n_{p}} \times v_{p}\] where, \[n_{p}\] = number of turns in the primary \[n_{s}\] = number of. A source (or primary) inductor (ls) and a load (or secondary) inductor (ll). Each inductor loop is in. Web as the transformer is basically a linear device, a ratio now exists between the number of turns of the primary coil divided by.

Formula Sheet 2 Transformer Where N1 are the voltage and number of

Equivalent resistance of transformer windings: \[v_{s} = \frac{n_{s}}{n_{p}} \times v_{p}\] where, \[n_{p}\] = number of turns in the primary \[n_{s}\] = number of. A source (or primary) inductor (ls) and a load (or secondary) inductor (ll). Web figure 1 as seen in figure 1, the transformer has two inductors: Emf induced in primary & secondary windings:

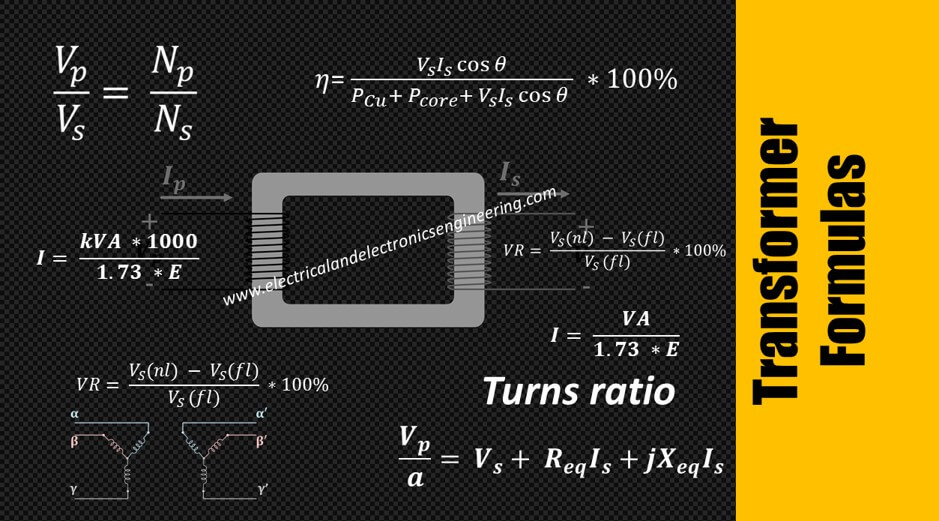
Top 10 Transformer Formulas Electrical and Electronics Engineering

Equivalent resistance of transformer windings: A source (or primary) inductor (ls) and a load (or secondary) inductor (ll). Emf induced in primary & secondary windings: Web figure 1 as seen in figure 1, the transformer has two inductors: Web as the transformer is basically a linear device, a ratio now exists between the number of turns of the primary coil.

Web Figure 1 As Seen In Figure 1, The Transformer Has Two Inductors:

Emf induced in primary & secondary windings: Equivalent resistance of transformer windings: Web as the transformer is basically a linear device, a ratio now exists between the number of turns of the primary coil divided by the number of turns of the secondary coil. Each inductor loop is in.