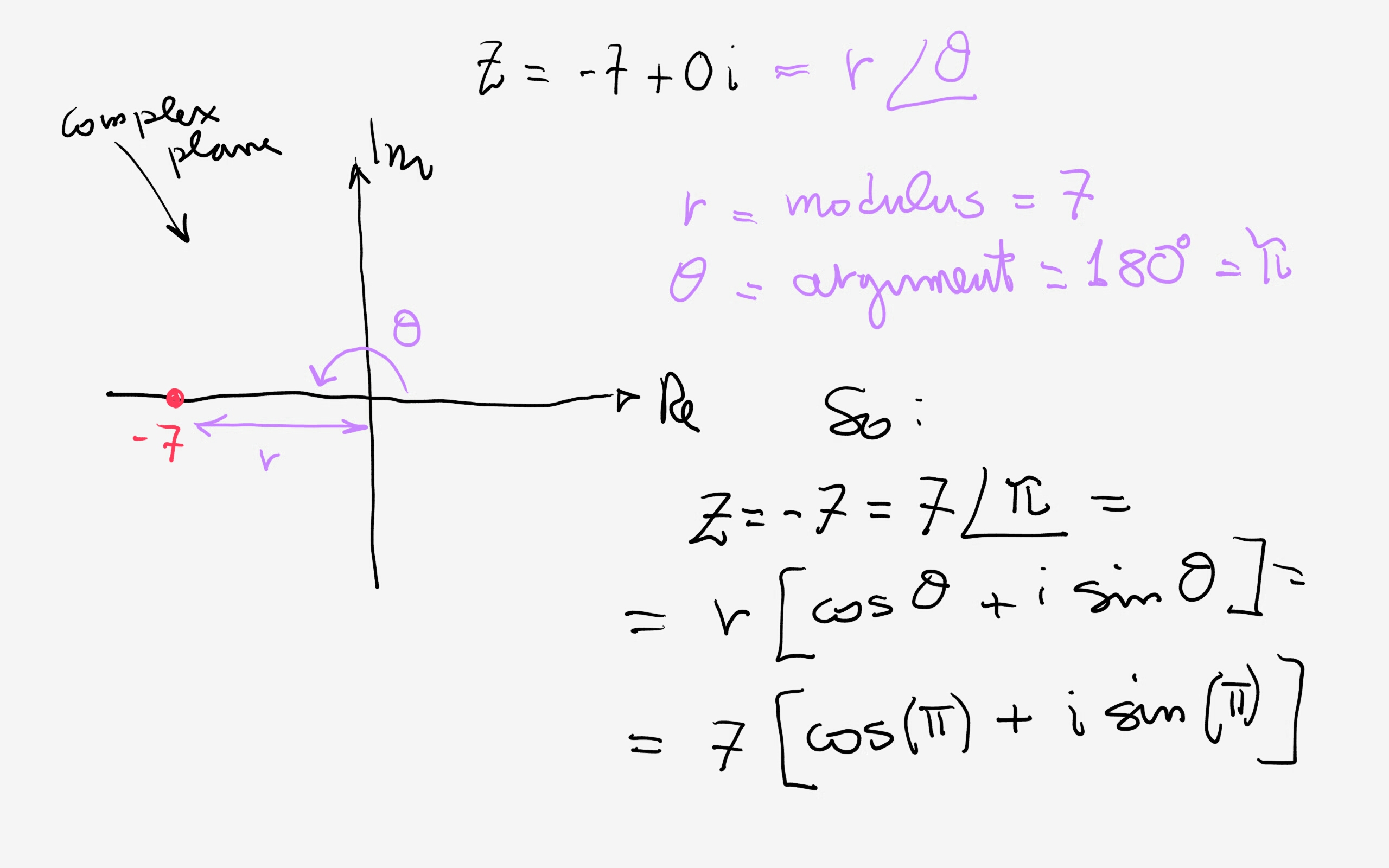Trigonometric Form Of Complex Numbers
Trigonometric Form Of Complex Numbers - The trigonometric form of a complex number products of complex numbers in polar form. Web the trigonometric form of a complex number contains the modulus, r, and the argument, θ, representing the complex number. Quotients of complex numbers in polar form. This complex exponential function is sometimes denoted cis x (cosine plus i sine). Let's compute the two trigonometric forms: This is the trigonometric form of a complex number where |z| | z | is the modulus and θ θ is the angle created on the complex plane. Ppp =16 + 16 =32 = 42 4 tan ==1 43 =; Depending on what you need to do with your complex numbers, the trigonometric form can be very useful or very thorny. There is an important product formula for complex numbers that the polar form. We have seen that we multiply complex numbers in polar form by multiplying.
Bwherer=ja+bij is themodulusofz, and tan =a. Ppp =16 + 16 =32 = 42 4 tan ==1 43 =; = a + bi becomes z = r(cos + isin ) = |z| and the reference angle, ' is given by tan ' = |b/a| note that it is up to you to make sure is in the correct quadrant. Web trigonometric polar form of a complex number describes the location of a point on the complex plane using the angle and the radius of the point. Web the trigonometric form of a complex number contains the modulus, r, and the argument, θ, representing the complex number. Quotients of complex numbers in polar form. Normally,we will require 0 complex numbers</strong> in trigonometric form: The trigonometric form of a complex number products of complex numbers in polar form. 4 + 4i to write the number in trigonometric form, we needrand. Depending on what you need to do with your complex numbers, the trigonometric form can be very useful or very thorny.
We have seen that we multiply complex numbers in polar form by multiplying. Web the trigonometric form of a complex number contains the modulus, r, and the argument, θ, representing the complex number. Bwherer=ja+bij is themodulusofz, and tan =a. You will use the distance from the point to the origin as r and the angle that the point makes as \(\theta \). From the graph, we can see how the trigonometric or polar forms of complex numbers were derived. This is the trigonometric form of a complex number where |z| | z | is the modulus and θ θ is the angle created on the complex plane. Normally,we will require 0 complex numbers</strong> in trigonometric form: Let's compute the two trigonometric forms: = a + bi becomes z = r(cos + isin ) = |z| and the reference angle, ' is given by tan ' = |b/a| note that it is up to you to make sure is in the correct quadrant. Web trigonometric polar form of a complex number describes the location of a point on the complex plane using the angle and the radius of the point.
PPT 10.4 Trigonometric (Polar) Form of Complex Numbers PowerPoint
Let's compute the two trigonometric forms: Web thetrigonometric formof a complex numberz=a+biis =r(cos +isin ); There is an important product formula for complex numbers that the polar form. The general trigonometric form of complex numbers is r ( cos θ + i sin θ). This complex exponential function is sometimes denoted cis x (cosine plus i sine).
PPT Trigonometric Form of a Complex Number PowerPoint Presentation
Web why do you need to find the trigonometric form of a complex number? Web trigonometric form of a complex number. Where e is the base of the natural logarithm, i is the imaginary unit, and cos and sin are the trigonometric functions cosine and sine respectively. From the graph, we can see how the trigonometric or polar forms of.
Complex Numbers in Trigonometric Form YouTube
Where e is the base of the natural logarithm, i is the imaginary unit, and cos and sin are the trigonometric functions cosine and sine respectively. Let's compute the two trigonometric forms: Normally,we will require 0 complex numbers</strong> in trigonometric form: Ppp =16 + 16 =32 = 42 4 tan ==1 43 =; = a + bi becomes z =.
PPT Trigonometric Form of a Complex Number PowerPoint Presentation
You will use the distance from the point to the origin as r and the angle that the point makes as \(\theta \). = a + bi becomes z = r(cos + isin ) = |z| and the reference angle, ' is given by tan ' = |b/a| note that it is up to you to make sure is in.
PPT Trigonometric Form of a Complex Number PowerPoint Presentation
You will use the distance from the point to the origin as r and the angle that the point makes as \(\theta \). Web trigonometric form of a complex number. The trigonometric form of a complex number products of complex numbers in polar form. Ppp =16 + 16 =32 = 42 4 tan ==1 43 =; Web the trigonometric form.
PPT Trigonometric Form of a Complex Number PowerPoint Presentation
Web why do you need to find the trigonometric form of a complex number? = a + bi becomes z = r(cos + isin ) = |z| and the reference angle, ' is given by tan ' = |b/a| note that it is up to you to make sure is in the correct quadrant. Ppp =16 + 16 =32 =.
The Product and Quotient of Complex Numbers in Trigonometric Form YouTube
Where e is the base of the natural logarithm, i is the imaginary unit, and cos and sin are the trigonometric functions cosine and sine respectively. The general trigonometric form of complex numbers is r ( cos θ + i sin θ). Quotients of complex numbers in polar form. Web the trigonometric form of a complex number contains the modulus,.
How do you write the complex number in trigonometric form 7? Socratic
Bwherer=ja+bij is themodulusofz, and tan =a. Depending on what you need to do with your complex numbers, the trigonometric form can be very useful or very thorny. The general trigonometric form of complex numbers is r ( cos θ + i sin θ). Let's compute the two trigonometric forms: This is the trigonometric form of a complex number where |z|.
How do you express the complex number in trigonometric form 2+(sqrt 3
You will use the distance from the point to the origin as r and the angle that the point makes as \(\theta \). There is an important product formula for complex numbers that the polar form. = a + bi becomes z = r(cos + isin ) = |z| and the reference angle, ' is given by tan ' =.
Trigonometric Form Into A Complex Number
This is the trigonometric form of a complex number where |z| | z | is the modulus and θ θ is the angle created on the complex plane. = a + bi becomes z = r(cos + isin ) = |z| and the reference angle, ' is given by tan ' = |b/a| note that it is up to you.
Normally,We Will Require 0 Complex Numbers</Strong> In Trigonometric Form:
There is an important product formula for complex numbers that the polar form. Let's compute the two trigonometric forms: Web trigonometric form of a complex number. You will use the distance from the point to the origin as r and the angle that the point makes as \(\theta \).
From The Graph, We Can See How The Trigonometric Or Polar Forms Of Complex Numbers Were Derived.
4 + 4i to write the number in trigonometric form, we needrand. Web euler's formula states that for any real number x : Where e is the base of the natural logarithm, i is the imaginary unit, and cos and sin are the trigonometric functions cosine and sine respectively. We have seen that we multiply complex numbers in polar form by multiplying.
= A + Bi Becomes Z = R(Cos + Isin ) = |Z| And The Reference Angle, ' Is Given By Tan ' = |B/A| Note That It Is Up To You To Make Sure Is In The Correct Quadrant.
Depending on what you need to do with your complex numbers, the trigonometric form can be very useful or very thorny. The general trigonometric form of complex numbers is r ( cos θ + i sin θ). Put these complex numbers in trigonometric form. Bwherer=ja+bij is themodulusofz, and tan =a.
Ppp =16 + 16 =32 = 42 4 Tan ==1 43 =;
This complex exponential function is sometimes denoted cis x (cosine plus i sine). For example, let z1 = 1 + i, z2 = √3 +i and z3 = −1 +i√3. Web trigonometric polar form of a complex number describes the location of a point on the complex plane using the angle and the radius of the point. Web the trigonometric form of a complex number contains the modulus, r, and the argument, θ, representing the complex number.